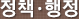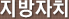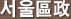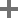мҲҳн•ҷмқ„ кіөл¶Җн•ҳлӢӨ ліҙл©ҙ мЈјм–ҙ진 м—¬лҹ¬ к°ңмқҳ ліҙкё°лҘј ліҙкі , кіөнҶөлҗң к·ңм№ҷмқ„ м°ҫм•„ лӢөмқ„ м°ҫм•„лӮҙм•ј н•ҳлҠ” л¬ём ңк°Җ л§ҺмҠөлӢҲлӢӨ. мқҙлІҲм—җлҠ” мқҙлҹ¬н•ң мҲҳн•ҷм Ғ к·ңм№ҷмқ„ м°ҫм•„ л¬ём ңлҘј н•ҙкІ°н•ҙ ліҙлҸ„лЎқ н•ҳкІ мҠөлӢҲлӢӨ. лҚ§м…Ҳ, лә„м…Ҳ, кіұм…Ҳ, лӮҳлҲ—м…Ҳмқ„ мқҙмҡ©н•ҳм—¬ лӢӨм–‘н•ң к°ҒлҸ„лЎң мғқк°Ғн•ҙ ліҙм„ёмҡ”.
л¬ём ң : к·ңм№ҷмқ„ м°ҫм•„ ?м—җ л“Өм–ҙк°Ҳ мҲ«мһҗлҘј кө¬н•ҳмӢңмҳӨ.
в—Ҹн•ҙлӢө
(1) 7(7Г—1)вҶ’14(7Г—2)вҶ’21(7Г—3)вҶ’28(7Г—4)вҶ’35(7Г—5),9(9Г—1)вҶ’18(9Г—2)вҶ’27(9Г—3)вҶ’36(9Г—4)вҶ’45(9Г—5),3(3Г—1)вҶ’6(3Г—2)вҶ’9(3Г—3)вҶ’12(3Г—4)вҶ’15(3Г—5)лЎң к·ңм№ҷмқ„ м°ҫм•„ліҙл©ҙ мӮ¬к°Ғнҳ•мқҳ мҷјмӘҪ мң„л¶Җн„° мӢңкі„л°©н–ҘмңјлЎң мҷјмӘҪ мң„мқҳ мҲҳм—җ кіұн•ҳкё° 1,2,3,4лҘј н•ң л’Ө к°ҖмҡҙлҚ°лҠ” кіұн•ҳкё° 5лҘј н•©лӢҲлӢӨ.
л”°лқјм„ң,12(12Г—1)вҶ’24(12Г—2)вҶ’?(12Г—3)вҶ’48(12Г—4)вҶ’60(12Г—5)мңјлЎң ?лҠ” 12Г—3=36мһ…лӢҲлӢӨ.
(2) (9+3+5)Г—2=17Г—2=34,(4+7+1)Г—2=12Г—2=24,(2+10+6)Г—2=18Г—2=36мңјлЎң к·ңм№ҷмқ„ м°ҫм•„ліҙл©ҙ мӮјк°Ғнҳ•мқҳ м„ё кјӯ짓м җм—җ мһҲлҠ” мҲҳл“Өмқҳ н•©м—җ кіұн•ҳкё° 2лҘј н•ң кІғмһ…лӢҲлӢӨ.
л”°лқјм„ң,2+?+6=32Г·2 вҶ’ 2+?+6=16 вҶ’ ?=8
(3) (5Г—6)-(7-4)=30-3=27,(6Г—7)-(9-7)=42-2=40,(8Г—9)-(5-4)=71 лЎң к·ңм№ҷмқҖ мӮ¬к°Ғнҳ• л°–мқҳ л‘җ мҲҳлҘј кіұн•ң нӣ„ мӮ¬к°Ғнҳ• м•Ҳмқҳ мҷјмӘҪ м•„лһҳмҷҖ мҳӨлҘёмӘҪ мң„мқҳ л‘җ мҲҳмқҳ м°ЁлҘј л№јмЈјл©ҙ к°ҖмҡҙлҚ° мҲҳк°Җ лҗ©лӢҲлӢӨ.
л”°лқјм„ң,(9Г—4)-(5-3)=36-2=34,?лҠ” 34мһ…лӢҲлӢӨ.
(4) 72+55-83-37=7,32+18-22-21=7,9+8-3-5=9лЎң к·ңм№ҷмқ„ м°ҫм•„ліҙл©ҙ к°ҖмҡҙлҚ° мҲҳлҠ” мң„мҷҖ мҳӨлҘёмӘҪмқҳ мҲҳлҘј н•©н•ҳкі , мҷјмӘҪкіј м•„лһҳмӘҪмқҳ мҲҳлҘј л№јмЈјл©ҙ лҗ©лӢҲлӢӨ. л”°лқјм„ң,16+55-23-8=40
м„ңмҡёкёҲлҸҷмҙҲл“ұн•ҷкөҗ көҗмӮ¬ мһ„м°Ҫк·